傅里叶变换
傅里叶变换的提出
电磁信号是时间的函数,不同的时间对应不同的强度。实际上,电磁信号也是频率的函数。频域是信号分析中的基本概念。
从时间函数的观念来看,一个信号可以是模拟的或是数字的。在一段时间内,信号强度变化是平滑的,没有中断或不连续,这种信号就称为模拟信号。如果一个信号在某一时段内强度保持某个常量值,在下一时段又变成另一个常量值,这种信号就称为数字信号。
周期信号是一种便于分析的简单信号,正弦波是最基本的模拟周期信号,可以用3个参数来表示:振幅\(A\)、频率\(f\)和相位\(\theta\),即
一个电磁信号通常不可能这么简单,如
这个信号是由频率为\(f\)和\(3f\)的正弦波组成的,如Fig.1所示。
Fig.1
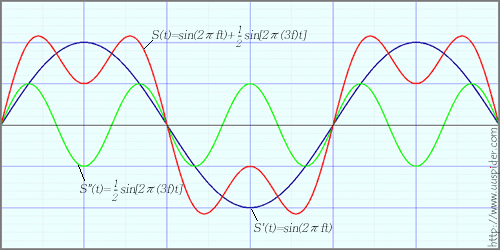
这个信号仍然是一个很简单的信号,那么更复杂的信号应该怎么分析呢?是不是也可以做类似的分解呢?这就是傅里叶变换要解决的问题之一。
傅里叶,Jean Baptiste Joseph Fourier(1768-1830),法国数学家、物理学家,傅里叶详细研究了热传导过程,于1807年在法国科学学会上提交了一篇论文,运用正弦曲线来描述温度分布,论文里有个在当时具有争议性的观点:任何连续周期信号可以由一组适当的正弦曲线组合而成。傅里叶没有做出严格的数学论证。这篇论文的审稿人中,有历史上著名的数学家拉格朗日(Joseph Louis Lagrange, 1736-1813)和拉普拉斯(Pierre Simon de Laplace, 1749-1827),当拉普拉斯和其它审稿人投票通过并要发表这篇论文时,拉格朗日坚决反对,认为傅里叶的方法无法表示带有棱角的信号。法国科学学会屈服于拉格朗日的威望,拒绝了傅里叶的工作,直到拉格朗日死后15年这篇论文才被发表出来。
拉格朗日是对的:正弦曲线无法组合成一个带有棱角的信号。但是,我们可以用正弦曲线来非常逼近地表示它,逼近到两种表示方法不存在能量差别,基于此,傅里叶是对的。
用正弦曲线来代替原来的曲线而不用方波或三角波来表示的原因在于,分解信号的方法是无穷的,但分解信号的目的是为了更加简单地处理原来的信号。用正余弦来表示原信号会更加简单,因为正余弦拥有原信号所不具有的性质:正弦曲线保真度。一个正弦曲线信号输入后,输出的仍是正弦曲线,只有幅度和相位可能发生变化,但是频率和波的形状仍是一样的。且只有正弦曲线才拥有这样的性质,正因如此我们才不用方波或三角波来表示。
傅里叶变换的意义
傅里叶变换是数字信号处理领域一种很重要的算法。要知道傅里叶变换算法的意义,首先要了解傅里叶原理的意义。傅里叶原理表明:任何连续测量的时序或信号,都可以表示为不同频率的正弦波信号的无限叠加。而根据该原理创立的傅里叶变换算法利用直接测量到的原始信号,以累加方式来计算该信号中不同正弦波信号的频率、振幅和相位。
和傅里叶变换算法对应的是反傅里叶变换算法。该反变换从本质上说也是一种累加处理,这样就可以将单独改变的正弦波信号转换成一个信号。因此,可以说,傅里叶变换将原来难以处理的时域信号转换成了易于分析的频域信号,可以利用一些工具对这些频域信号进行处理、加工。最后还可以利用傅里叶反变换将这些频域信号转换成时域信号。
从现代数学的眼光来看,傅里叶变换是一种特殊的积分变换。通过一定的分解,”任意”的函数都能够表示为正弦函数的线性组合的形式,而正弦函数是被充分研究而相对简单的函数类。
正是由于上述的良好性质,傅里叶变换在物理学、电子类学科、数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学、海洋学、结构动力学等领域都有着广泛的应用。
傅里叶变换
\(f(t)\)是\(t\)的周期函数,如果\(t\)满足一定的条件(狄里赫来条件),则有:
傅里叶变换
$$ F(\omega )=\cal F \it [f(t)]=\int_{- \infty }^{ \infty } f(t) e^{ -i \omega t}{\rm d}t $$
以及,傅里叶逆变换
$$ f(t)=\cal F \it ^{-1} [F(\omega )]=\frac{1}{2 \pi } \int_{- \infty }^{ \infty } F(\omega ) e^{ i \omega t}{\rm d} \omega $$
\(F(\omega )\)叫做\(f(t)\)的像函数,\(f(t)\)叫做\(F(\omega )\)的像原函数,\(F(\omega )\)是\(f(t)\)的像,\(f(t)\)是\(F(\omega )\)的原像。