相控阵雷达
“相控阵”是“相位控制阵列”的简称,相控阵雷达的关键部件是相控阵天线。相控阵天线由大量辐射单元排列而成,通过调节各个单元的馈电相位实现对天线波束的控制。
1. 相控阵原理
相控阵天线的辐射单元少则几百,多则成千上万。每个阵元(或一组阵元)都与一个可控移相器连接,通过控制移相器的相移量,可以改变各单元间的相对馈电相位,从而改变天线阵面上电磁波的相位分布,促使波束在空间按预定程序扫描。
下面以线阵列天线为例来说明相位扫描的原理。
如图所示,由\(N\)个阵元组成的一维直线天线阵,阵元间距为\(d\)。假定各辐射单元为无方向性的点辐射源,而且同相、等幅馈电,以0号阵元为相位基准,各移相器的相移量可分别记作\(0\),\( \varphi\),\( 2\varphi\),…,\( k \varphi\),…,\((N-1) \varphi\)。偏离天线阵法线\(\theta\)方向上两个振子之间波程差引起的相位差为
\(\psi = \frac{2 \pi}{\lambda} d \sin \theta\)
根据欧拉公式\(\cos \alpha+ i \sin \alpha = e ^{j\alpha}\),第\(k\)个振子在\(\theta\)方向远区某点辐射场矢量可记作:
\(E _k [\cos k (\psi - \varphi ) + i \sin k (\psi - \varphi ) ] = E _k e ^{jk(\psi - \varphi )}\)
因此,\(N\)个振子在\(\theta\)方向远区某点辐射场的矢量和为
\(E (\theta) = \Sigma ^{N-1} _{k=0} E _k e ^{jk (\psi - \varphi )} \)
远区各阵元的辐射场强可视作相等,记作\(E\),即\(E _k = E\),上式可简化为
\(E (\theta) = E \Sigma ^{N-1} _{k=0} e ^{jk (\psi - \varphi )} \)
当\(\varphi =0\)时,在天线阵法线方向上,各阵元的辐射场同相迭加可获得最大值,天线阵波束方向就是\(\theta=0\)的方向。
当\(\varphi \neq 0\)时,由于各单元之间相对的相位差不为零,天线阵的法线方向上各单元的辐射场不能同相相加,因而不是最大的辐射方向,天线阵波束发生偏转。
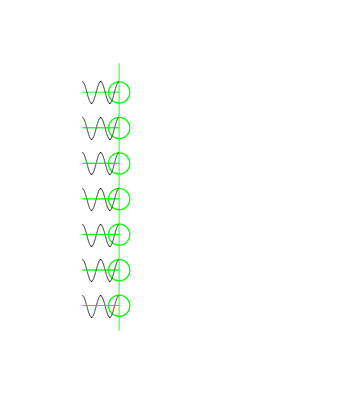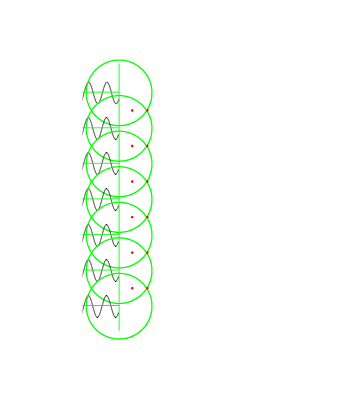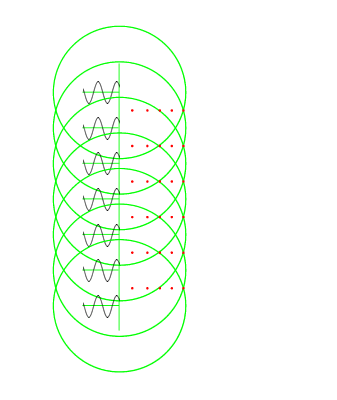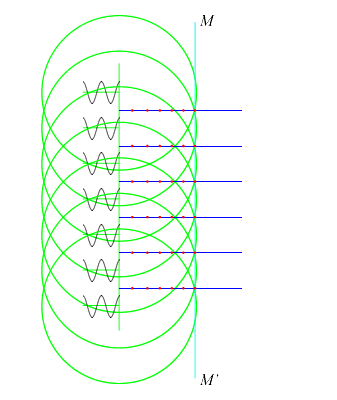
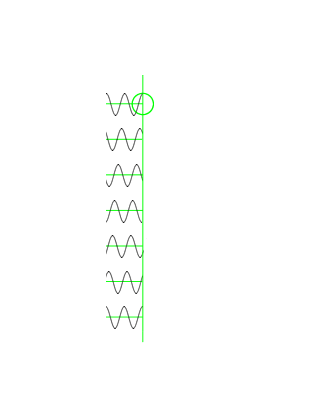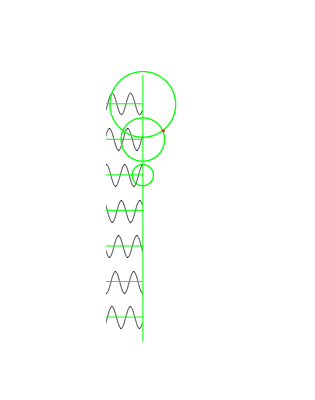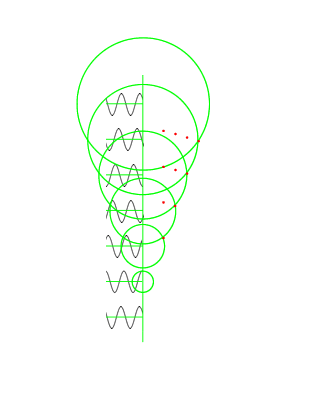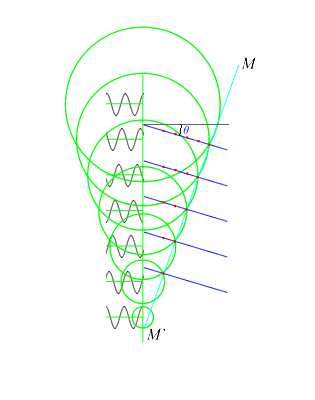
如果要使天线阵波束指向\(\theta _1\)方向,各相邻阵元发射的电磁波的波程差需要满足\( d \sin \theta _1\),因此,相邻阵元之间的相位差就应调整为\(\varphi _1 = \psi _1 = \frac{2 \pi}{\lambda} d \sin \theta _1\)。图中,\(MM’\)线上各电磁波的相位是相同的,称作同相波前,天线阵波束方向与其同相波前垂直。
可见,通过控制各移相器的相移量,同相波前倾斜,就改变了天线阵的波束指向,连续调节移相器就实现了天线阵波束扫描,这就是相位扫描的原理,即:
\(E (\theta) = E \Sigma ^{N-1} _{k=0} e ^{jk (\psi - \varphi) } \)
当\(\psi - \varphi = 0 \)时,有\( \left| E _{max} (\theta) \right| = NE \)。
在实际的相控阵雷达中,辐射单元一般排列在一个平面上,天线阵波束在仰角和方位上均可作相位扫描,也就是说通过相位控制可以使天线阵波束指向空中任意某个方向。
2. 栅瓣
计算\(E (\theta) = E \Sigma ^{N-1} _{k=0} e ^{jk (\psi - \varphi) } \)需要用到等比数列求和公式。
若\(a _n = a _1 \times q ^{(n-1)}\),则\(\Sigma ^n _1 a _n = \frac{a _1 (1-q ^n)}{1-q} \),在这里,\(a _1 = E e ^{j \cdot 0 (\psi - \varphi )} = E\),\(q = e ^{j (\psi - \varphi ) }\),为简化形式,令\(\phi = \psi - \varphi\),也就是\(q = e ^{j \phi }\),因此
\(E (\theta) = E \frac{1 - e ^{jN \phi } }{1 - e ^{j \phi } } \)
转换一下形式:
\(1 - e ^{jN \phi } = e ^{j \frac{N}{2} \phi } (e ^{- j \frac{N}{2} \phi } - e ^{j \frac{N}{2} \phi })\)
\(= e ^{j \frac{N}{2} \phi } [\cos (-\frac{N}{2} \phi) + i\sin (-\frac{N}{2} \phi) - \cos \frac{N}{2} \phi - i \sin \frac{N}{2} \phi ]\)
\(= e ^{j \frac{N}{2} \phi } (- i \cdot 2 \sin \frac{N}{2} \phi) \)
同理:
\(1 - e ^{j \phi } = e ^{j \frac{1}{2} \phi } (e ^{- j \frac{1}{2} \phi } - e ^{j \frac{1}{2} \phi })\)
\(= e ^{j \frac{1}{2} \phi } [\cos (-\frac{1}{2} \phi) + i\sin (-\frac{1}{2} \phi) - \cos \frac{1}{2} \phi - i \sin \frac{1}{2} \phi ]\)
\(= e ^{j \frac{1}{2} \phi } (- i \cdot 2 \sin \frac{1}{2} \phi) \)
因此,可以得到:
\(E (\theta) = E \frac{1 - e ^{jN \phi } }{1 - e ^{j \phi } } \)
\( = E \frac{\sin \frac{N}{2} \phi }{\sin \frac{1}{2} \phi } e ^{j \frac{N-1}{2} \phi }\)
\( = E \frac{\sin \frac{N}{2} (\psi - \varphi) }{\sin \frac{1}{2} (\psi - \varphi) } e ^{j \frac{N-1}{2} (\psi - \varphi) }\)
天线阵波束归一化方向性函数为
\(F (\theta ) = \frac{|E(\theta )|}{|E _{max} (\theta )| } = \left| \frac{1}{N} \frac{sin[\frac{N}{2}(\psi - \varphi )]}{sin[\frac{1}{2}(\psi - \varphi )]}\right|\)
\(= \left| \frac{1}{N} \frac{sin[\frac{N}{2}(\frac{2 \pi}{\lambda }d \sin \theta - \varphi )]}{sin[\frac{1}{2}(\frac{2 \pi}{\lambda }d \sin \theta - \varphi )]}\right|\)
当波束方向与法线夹角为\(\theta _1\)时,需要满足\(\varphi = \frac{2 \pi}{\lambda} d \sin \theta _1\),此时有
\(F(\theta ) = \left| \frac{1}{N} \frac{sin[\frac{N \pi d}{\lambda }(\sin \theta - \sin \theta _1)]}{sin[\frac{\pi d}{\lambda }(\sin \theta - \sin \theta _1)]}\right|\)
当\(\frac{N \pi d}{\lambda }(\sin \theta - \sin \theta _1 ) = n \pi \)(\(n\)为整数)时,分子为零,若分母不为零,则\(F(\theta ) = 0 \);
当\(\frac{\pi d}{\lambda }(\sin \theta - \sin \theta _1 ) = n \pi \)(\(n\)为整数)时,分子、分母同时为零,根据洛必达法则,\(F(\theta ) = 1 \),为最大值。由于\(n\)的取值不唯一,\(F(\theta ) \)的表现为多瓣状,其中,当\(n = 0\),即\(\theta = \theta _1\)时称作主瓣,当\(n\)为其它整数时称作栅瓣。
栅瓣导致了测角的多值性问题,为了避免栅瓣的出现,需要
\(\frac{\pi d}{\lambda } \left| \sin \theta - \sin \theta _1 \right| < \pi \)
因为
\(\left| \sin \theta - \sin \theta _1\right| \leq \left| \sin \theta \right| + \left| \sin \theta _1 \right| \leq 1 + \left| \sin \theta _1 \right| \)
所以,不出现栅瓣的条件就是
\(\frac{d}{\lambda } < \frac{1}{1 + \left| \sin \theta _1 \right|} \)
若\(\lambda \)确定,只要调整阵元间距\(d\)满足上式,就不会出现栅瓣,通常取\(\frac{d}{\lambda } \leq \frac{1}{2} \)。
3. 波束宽度
3.1 \( \theta _1 = 0\)
若天线阵波束指向与阵面法线方向相同时,则
\(F(\theta ) = \left| \frac{1}{N} \frac{\sin(\frac{N \pi d}{\lambda }\sin \theta )}{\sin(\frac{\pi d}{\lambda }\sin \theta )}\right|\)
波束很窄时,\(\left| \theta \right|\)很小,\(\sin (\frac{\pi d}{\lambda } \sin \theta ) \approx \frac{\pi d}{\lambda} \sin \theta\),因此
\(F(\theta ) = \left| \frac{1}{N} \frac{\sin(\frac{N \pi d}{\lambda }\sin \theta )}{\frac{N \pi d}{\lambda }\sin \theta }\right|\)
该式近似为Sinc函数,由此可求出波束半功率宽度为
\(\theta _{0.5} \approx \frac{0.886}{Nd} \lambda (rad) \approx \frac{50.8}{Nd} \lambda (\circ ) \)
其中\(Nd\)为线阵长度,当\(d = \frac{\lambda}{2}\)时,\(\theta _{0.5} \approx \frac{100}{N} (\circ ) \)。
若要求\(\theta _{0.5} = 1(\circ ) \),可以计算出阵列单元的数目\(N = 100\)。
3.2 \( \theta _1 \neq 0\)
波束很窄时,\(\left| \theta - \theta _1 \right|\)很小,因此
\(\sin [\frac{\pi d}{\lambda} (\sin \theta - \sin \theta _1)] \approx \frac{\pi d}{\lambda} (\sin \theta - \sin \theta _1 )\)
由此得到
\(F(\theta ) = \left| \frac{\sin [\frac{N \pi d}{\lambda} (\sin \theta - \sin \theta _1)]}{\frac{N \pi d}{\lambda} (\sin \theta - \sin \theta _1)}\right|\)
该式为Sinc函数,查表,当\(\frac{\sin x}{x} = 0.707\)时,\(x = \pm 0.443 \pi \),即\(\theta = \theta _+\)时有
\(\frac{N \pi d }{\lambda} (\sin \theta _+ - \sin \theta _1) = 0.443 \pi \)
上式中
\( \sin \theta _+ - \sin \theta _1 = \sin (\theta _+ - theta _1) \cos \theta _1 - [1 - \cos (\theta _+ - \theta _1)] \sin \theta _1 \)
波束很窄时,\(\theta _+ - \theta _1\)很小,因此
\(\sin \theta _+ - \sin \theta _1 \approx (\theta _+ - \theta _1) \cos \theta _1\)
由此可得
\(\frac{N \pi d }{\lambda} (\theta _+ - \theta _1) \cos \theta _1 = 0.443 \pi \)
因此波束宽度为
\(\theta _{0.5s} = 2 (\theta _+ - \theta _1) \approx \frac{0.886}{Nd \cos \theta _1} \lambda (rad) \approx \frac{50.8}{Nd \cos \theta _1} \lambda (\circ ) = \frac{\theta _{0.5} }{\cos \theta _1}\)
可见,波束扫描时,若\(\theta _1\)增大,则\(\theta _{0.5s}\)展宽,导致天线增益下降。
记法线方向天线增益为
\(G (0) = \frac{4 \pi A}{\lambda ^2} = \frac{4 \pi N _0 d ^2}{\lambda ^2}\)
当波束扫描到\(\theta _1\)方向时,天线发射或接收能量的有效口径面积\(A _s\)为\(A\)在扫描等相位面上的投影,即
\(A _s = A \cos \theta _1 = N _0 d ^2 \cos \theta _1 \)
由此得到
\(G (\theta _1) = \frac{4 \pi A _s}{\lambda ^2} = \frac{4 \pi N _0 d ^2}{\lambda ^2} \cos \theta _1 \)
可见,当\(\theta _1\)增大时,\(G(\theta _1)\)将减小,通常取\(\theta _1\)在\(\pm 60 \circ\)或\(\pm 45 \circ\)之间。
等间距和等幅馈电的阵列天线副瓣较大,增加天线阵中心阵元的功率(振幅加权)或阵元的密度(密度加权),可有效抑制副瓣。
4. 频率扫描
信号通过延迟线传输到天线阵列单元,调节信号的频率,也可以产生特定的相位差,形成可控的同相波前,实现波束扫描,这种方法称为频率扫描。频率扫描的成本较高,通常采用子阵技术,使一定数目的阵列单元组成子阵,每个阵元采用移相器控制,而每个子阵后加上延迟线,若干个子阵钩成整个天线阵列。频率扫描也存在波束展宽和增益下降的问题,也可以采用振幅加权和密度加权的方法来降低副瓣电平。
5. 相控阵雷达的特性
- 无惯性快速波束扫描
相控阵天线波束的扫描或转换时间,取决于移相器的转换速度,通常仅需几个微秒甚至更短,且不存在机械扫描难以避免的惯性。
- 独立波束控制
可控制一部分阵元产生一个波束,另一部分阵元产生另一个波束,各个波束可具有不同的辐射功率、波束宽度、目标驻留时间、重复频率、重复扫描次数等,这些波束可以分别控制,也可以统一控制。
- 空间功率合成
成千上万的阵列单元辐射的合成功率可达十几兆瓦,作用距离可达数千千米以上。
- 自适应能力
天线阵的波束可通过计算机灵活控制、转换和分析,借助强大的软件平台,大大提高了其智能化水平,同时,当部分阵列单元故障时,不会影响其他单元的正常工作,可以不停机维修和维护,具有很强的适应能力。
- 抗干扰
相控阵雷达的波束形状及其控制方式、脉冲重复频率和宽度、工作频率和调制方式都可以快速转换,可综合运用单脉冲、脉冲压缩、频率分集、频率捷变等雷达技术,既可提高检测精度,也提高了抗干扰性能。